一番下に、公立高校入試のしくみ・公立高校入試の傾向・LINKがあります。
【1】
次の各問に答えなさい。(65点)
(1) -4x + 7x を計算しなさい。(4点)
(2) (-2) × (-5) – 6 を計算しなさい。(4点)
(3) 48xy2 ÷ 3x ÷ 8y を計算しなさい。(4点)
(4) 方程式 2x + 12 = -3x – 8 を解きなさい。(4点)
(5) 21/√7 – √28 を計算しなさい。(4点)
(6) x2 – 13x + 40 を因数分解しなさい。(4点)
正解:
(1)●●●
(2)●●●
(3)●●●
(4)●●●
(5)●●●
(6)●●●
(7) 連立方程式を解きなさい。(4点)
3x - 7y = 5
5x - 2y = -11
(8) 2次方程式 2x2 – x – 9 = 0 を解きなさい。(4点)
(9) y は x に反比例し、x = 3 のとき y = 4 です。 このとき、y を x の式で表しなさい。(4点)
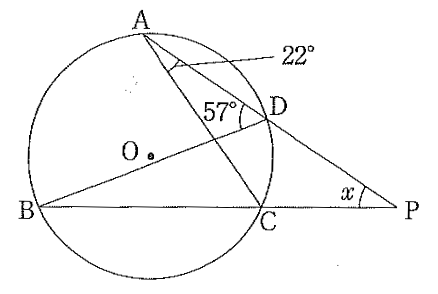
(10) 右の図のように、円 O の周上に 4 点 A、B、C、D をとり、直線 AD と直線 BC との交点を P とします。
∠CAD = 22°、∠ADB = 57° のとき、∠APB の大きさ x を求めなさい。(4点)
正解:
(7)●●●
(8)●●●
(9)●●●
(10)●●●
(11)次は、あるクラスの生徒21人に行ったテストの得点を小さい順に並べたものです。このデータから得られる値として誤っているものを、下のア~エの中から一つ選び、その記号を書きなさい。(4点)
テストの得点(点)
45, 48, 48, 52, 54, 54, 56, 60, 62, 65, 66, 68, 70, 72, 74, 74, 78, 80, 84, 86, 90
ア 中央値は 66 である。
イ 第1四分位数は 54 である。
ウ 第3四分位数は 74 である。
エ 分布の範囲は 45 である。
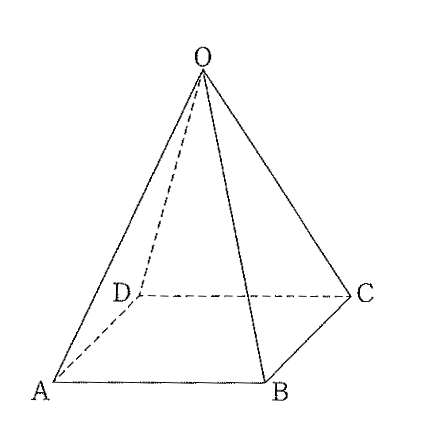
(12)右の図のような、正四角錐 OABCD があります。
底面が1辺の長さ6cmの正方形ABCDで、ほかの辺の長さがすべて12cmであるとき、この立体の体積を求めなさい。(4点)
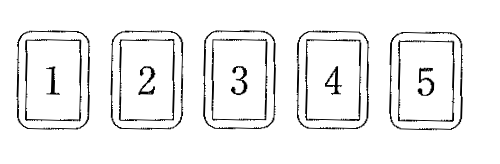
(13)右の図のような、5枚のカードがあります。
この5枚のカードを箱に入れて、そこから1枚ずつ合計で2枚取り出します。1枚目に取り出したカードの数をx、2枚目に取り出したカードの数をyとするとき、x/yの値が2/3以下となる確率を求めなさい。(4点)
ただし、箱の中は見えず、取り出したカードは箱に戻さないものとします。また、どのカードの取り出し方も同様に確からしいものとします。
正解:
(11)●●●
(12)●●●
(13)●●●
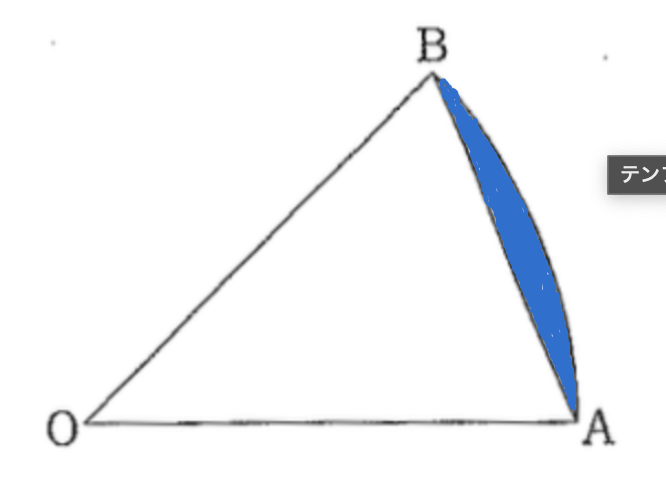
(14) 右の図のような, OA = OB = 4cm, ∠AOB = 45°のおうぎ形 OABがあります。線分ABをひくとき、青色(⬜︎)をつけた部分の面積を求めなさい。(4点)
(15) 連続する2つの自然数があります。それぞれを2乗した数の和が365になるとき、これら2つの自然数を求めなさい。(4点)
正解:
(14)●●●
Short解説はこちら
(15)●●●
(16) 次は、先生とSさん、Tさんの会話です。これを読んで、下の問に答えなさい。
先生「表1は、A中学校とB中学校の3年男子の反復横とびの結果を度数分布表にまとめたものです。2つの学校の結果を比較して、54回以上とんだ生徒の割合が大きいのはどちらの学校か考えてみましょう。」
Sさん「表1では、合計の人数が異なるね。どうしたら2つの学校の結果を比較できるかな。」
Tさん「各階級の相対度数を求めてその値を用いれば、比較できると思うよ。」
Sさん「そうだね。それでは、表1をもとに各階級の相対度数を求めてみよう。」
問 表2は、表1をもとにつくった相対度数の表です。表2中のアにあてはまる値を書きなさい。また、54回以上とんだ生徒の割合が大きいのはどちらの学校か、表2を用いて、具体的な値を示しながら説明しなさい。(5点)
| 階級(回) | A中学校 度数(人) | B中学校 度数(人) |
|---|---|---|
| 以上~未満 | ||
| 48~50 | 5 | 6 |
| 50~52 | 5 | 6 |
| 52~54 | 10 | 15 |
| 54~56 | 25 | 21 |
| 56~58 | 35 | 9 |
| 58~60 | 20 | 3 |
| 合計 | 100 | 60 |
表1
| 階級(回) | A中学校 相対度数 | B中学校 相対度数 |
|---|---|---|
| 以上~未満 | ||
| 48~50 | 0.05 | 0.10 |
| 50~52 | 0.05 | 0.10 |
| 52~54 | 0.10 | 0.25 |
| 54~56 | 0.25 | ア |
| 56~58 | 0.35 | 0.15 |
| 58~60 | 0.20 | 0.05 |
| 合計 | 1.00 | 1.00 |
表2
(16)●●●
【2】
次の各問に答えなさい。(11点)
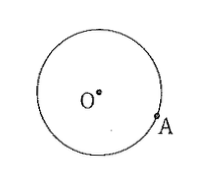
(1) 下の図のように、円Oの周上に点Aがあります。このとき、点Aを通る円Oの接線をコンパスと定規を使って作図しなさい。
ただし、作図するためにかいた線は、消さないでおきなさい。(5点)
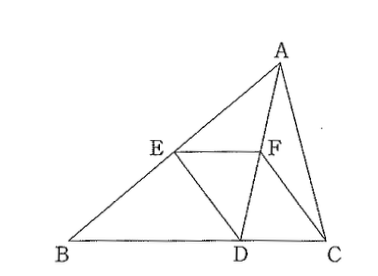
(2) 下の図のように、△ABCの辺BC上に点Dを、BD:DC=2:1となるようにとります。
辺AB, 線分ADの中点をそれぞれE、Fとするとき、四角形EDCFは平行四辺形であることを証明しなさい。(6点)
正解:
(1)●●●
(2)●●●
【3】
次は、先生とJさん、Kさんの会話です。これを読んで、あとの各問に答えなさい。(14点)
先生「下の図のように、はじめの2点の値をそれぞれ1,2として、次の操作を繰り返し行います。」
操作 円周上のとなり合う2点の間に点をとり、その点の値を、となり合う2点の値の和とします。
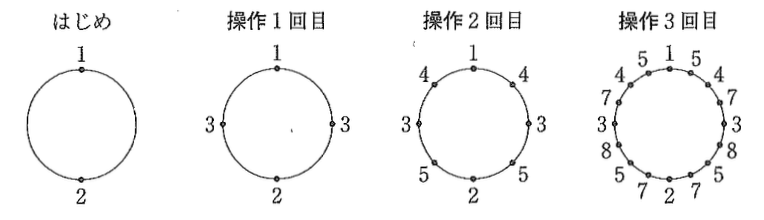
先生「このとき、円周上にある点の最大値と、円周上にあるすべての点の値の合計が、操作を繰り返し行うとどのように変化するか、その規則性を調べてみましょう。」
Jさん「操作3回目までの点の最大値と、すべての点の値の合計をまとめると、次のような表になりました。どんな規則性があるのでしょうか。」
| はじめ | 操作1回目 | 操作2回目 | 操作3回目 | |
| 点の最大値 | 2 | 3 | 5 | 8 |
| すべての点の値の合計 | 3 | 9 | 27 | 81 |
Kさん「Jさんがまとめた表を見ると、操作4回目における点の最大値はア、すべての点の値の合計はイになると思います。」
先生「正解です。」
Jさん「ところで、点の最大値や、すべての点の値の合計における変化の規則性は、はじめの2点の値を変えても同じなのでしょうか。」
先生「はじめの2点の値を変えてみるというのはよい視点ですね。それでは、はじめの2点の値をそれぞれ自然数のa,bに変えたときについて調べてみましょう。」
(1) ア , イ にあてはまる自然数を求めなさい。(4点)
(2) 下線部について、右の図は、A, Bをはじめの2点として、操作を2回行ったときの図です。操作1回目でとった点をC, D, 操作2回目でとった点をE, F, G, Hとします。Aの値をa, Bの値をbとするとき、円周上にあるすべての点の値の合計が、aとbの和の9倍になることを説明しなさい。(5点)

(3) はじめの2点の値をそれぞれ2, 5として操作をn回行い、円周上にあるすべての点の値の合計を求めたところ、1701になりました。このとき、nの値と点の最大値をそれぞれ求めなさい。(5点)
正解:
(1)●●●
(2)●●●
(3)●●●
【4】
4 図1で、曲線は関数y = (3/4)x²のグラフです。曲線上にx座標が-2, 4である2点A, Bをとり、この2点を通る直線lをひくとき、次の各問に答えなさい。(10点)

(1) 直線lの式を求めなさい。(4点)
(2) 図2のように、直線lとx軸との交点をC、点Bからx軸に垂線をひき、x軸との交点をDとします。また、曲線上の0
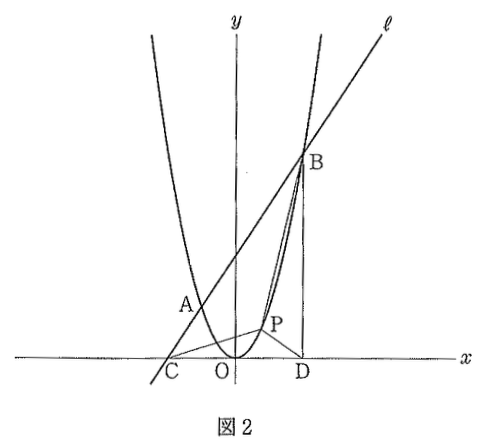
正解:
(1)●●●
(2)●●●
埼玉県教育委員会のホームページより、最新の情報が得られます。必要に応じて、見るようにしましょう!






