最後に、傾向と対策・高校入試のしくみなどへのLINKがあります。
【1】
次の1〜9に答えなさい。
- を計算しなさい。
- を計算しなさい。
- , のとき, の値を求めなさい。
- を計算しなさい。
- を因数分解しなさい。
- 関数 について, の変域が のとき, の変域を求めなさい。
- 関数 のグラフをかきなさい。
-
1から6までの目が出る2つのさいころA, Bを同時に投げる。さいころAの出る目の数を十の位の数,さいころBの出る目の数を一の位の数としてできる2けたの自然数が4の倍数になる確率を求めなさい。
ただし,さいころはどの目が出ることも同様に確からしいとする。 -
白の碁石だけがたくさん入っている袋がある。この袋に白の碁石と同じ大きさの黒の碁石を50個入れてよくかき混ぜ,この袋から30個の碁石を無作為に抽出したところ,黒の碁石は6個であった。
この袋に入っている白の碁石の個数は,およそ何個と推定できるか答えなさい。
正解:●●●
正解:●●●
正解:●●●
正解:●●●
正解:●●●
正解:●●●
正解:●●●
正解:●●●
正解:●●●
【2】
希さんは,K中学校の1年生,2年生,3年生のそれぞれの生徒を対象に,1日あたりの睡眠時間について調査した。
表は,K中学校の各学年のデータをそれぞれ度数分布表に整理したものである。
図は,K中学校の各学年のデータをそれぞれ箱ひげ図に表したものである。
表
| 階級(時間) | 度数(人) | ||
|---|---|---|---|
| 1年生 | 2年生 | 3年生 | |
| 以上 未満 | |||
| 5 ~ 6 | 3 | 4 | 8 |
| 6 ~ 7 | 8 | 15 | 19 |
| 7 ~ 8 | 19 | 18 | 37 |
| 8 ~ 9 | 23 | 17 | 12 |
| 9 ~ 10 | 19 | 10 | 7 |
| 10 ~ 11 | 7 | 2 | 0 |
| 計 | 79 | 66 | 83 |
図
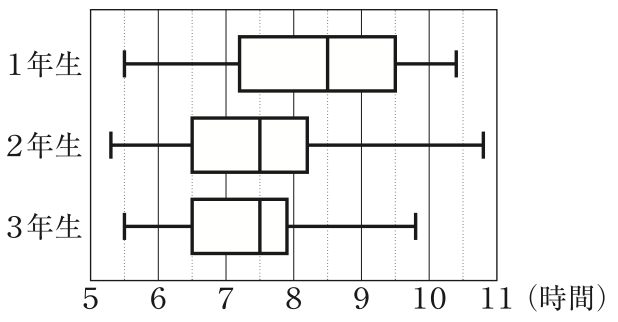
次の1〜3に答えなさい。
1.表において,各学年のデータの最頻値のうち,データの最頻値が最も大きい学年をかき,その学年のデータの最頻値を求めなさい。
正解:●●●
2.表や図から読みとれることとして,正しいことを述べているものを,次のア〜エから全て選び,記号をかきなさい。
ア K中学校で,睡眠時間が最も短い生徒は,2年生の中にいる。
イ 1年生において,睡眠時間が最も長い生徒と最も短い生徒で,5時間以上の差がある。
ウ 1年生と2年生において,睡眠時間が9.5時間以上の生徒の人数は,2年生の方が1年生より多い。
エ 3年生の生徒の睡眠時間を短い順に並べたとき,21番目の生徒の睡眠時間は,6.5時間である。
正解:●●●
3.表をもとに,睡眠時間が7時間未満の生徒の割合が最も大きいのは,どの学年であるかを,累積相対度数を用いて説明しなさい。
ただし,累積相対度数は四捨五入して小数第2位まで求めるものとする。
正解例:●●●
【3】
A「2をひく」,B「2倍する」,C「2乗する」,D「はじめの数をひく」という計算方法がかかれた4個の玉A, B, C, Dが袋に入っている。
この袋の中の玉を使って,次の手順によって,計算結果を求める。
手順
- 袋の中から玉を1個ずつ3回続けて取り出し,取り出した順に左から並べる。ただし,取り出した玉は袋にもどさない。
- はじめの数を1つ決める。
- はじめの数に対して,左の玉にかかれた計算を行う。
- ③で求めた数に対して,真ん中の玉にかかれた計算を行う。
- ④で求めた数に対して,右の玉にかかれた計算を行う。
図は,例えば,玉がA, B, Cの順に並んだ場合,はじめの数が1のとき,計算結果は4になることを表している。
図

下の会話文は,明さんと光さんが,手順によって,計算結果を求め,はじめの数,玉の並び方,計算結果の関係について話し合った内容の一部である。
 明さん
明さん玉がA, B, Cの順に並んだ場合,はじめの数が5のとき,計算結果は( Ⓟ )になるよ。
そうだね。はじめの数は5のままで,玉がB, A, Cの順に並んだ場合,計算結果は64になるので,はじめの数は変えずに,玉の並び方が変わると,計算結果は変わりそうだね。
 光さん
光さん
他にも,玉はB, A, Cの順に並んだままで,はじめの数を3に変えると,計算結果は16になるよ。このことから,玉の並び方が変わらずに,はじめの数を変えると,計算結果は変わりそうだね。
でも,調べてみたら,はじめの数をどんな数に変えても,計算結果が常に同じ数になる玉の並び方があるかもしれないよ。


どんな並び方かな。文字式を使って調べてみようよ。
次の1〜4に答えなさい。
1.手順①において,玉の並び方は全部で何通りあるか求めなさい。
正解:●●●
2.( Ⓟ ) にあてはまる数を求めなさい。また,玉が A, B, D の順に並んだ場合,計算結果が になるときの,はじめの数を求めなさい。
正解:●●●
3.明さんと光さんが,下線部について調べた結果,玉の並び方にはいずれもDがふくまれていることがわかった。その並び方のうち,真ん中の玉がDのときの玉の並び方と計算結果について,次のようにまとめた。
まとめ
真ん中の玉がDのとき,はじめの数をどんな数に変えても計算結果が常に同じ数になる玉の並び方と,そのときの計算結果の組み合わせは,次の2通りである。
・玉が ア, D, イ の順に並んだ場合,計算結果は常に ( Ⓠ ) になる。
・玉が ウ, D, エ の順に並んだ場合,計算結果は常に ( Ⓡ ) になる。
ア 〜 エ にあてはまる記号を,それぞれ A, B, C から選んでかきなさい。また,( Ⓠ ), ( Ⓡ ) にあてはまる数を求めなさい。
正解:●●●
4.玉が A, C, B の順に並んだ場合と,玉が B, C, A の順に並んだ場合について,はじめの数が同じ数で,それぞれの計算結果が等しくなるときの,はじめの数を全て求めなさい。
正解:●●●
【4】
A駅,B駅,C駅がこの順に一直線の線路上にあり,A駅からB駅までは4800m,A駅からC駅までは7200m離れている。電車Pは,午前8時にA駅を出発し,B駅に向かって一定の速さで12分間進み,B駅に到着した。B駅で3分間停車した後,B駅からC駅まで分速480mで進み,午前8時20分にC駅に到着した。
図は,午前8時から x 分後に電車PがA駅から y m離れているとするとき,午前8時から午前8時20分までの x と y の関係をグラフに表したものである。
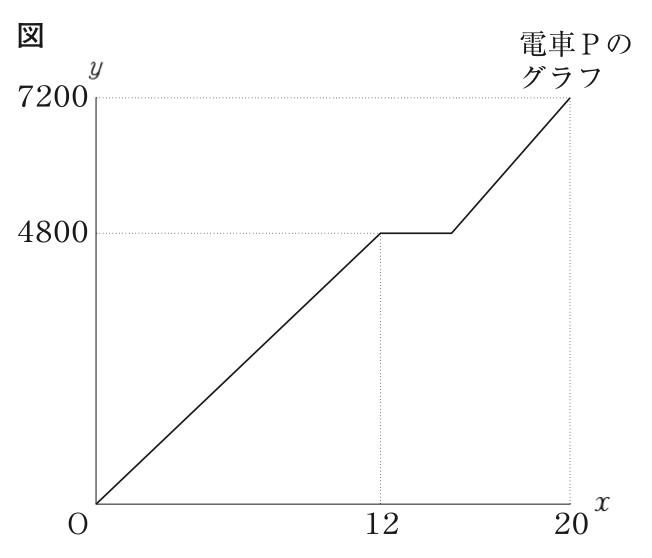
次の1〜4に答えなさい。
1.電車PがA駅から3000m離れているのは,電車PがA駅を出発してから何分何秒後か求めなさい。
正解:●●●
2.次のア〜エの表のうち,電車Pの午前8時16分から午前8時18分までの x と y の関係を正しく表したものが1つある。それを選び,記号をかきなさい。
正解:●●●
3.電車Qは,午前8時4分にA駅を出発し,A駅からC駅まで一定の速さで進む。電車Qは,電車PがB駅に到着した後にB駅を通過し,電車Pより早くC駅に到着した。このときの電車Qの速さについて,次のようにまとめた。
まとめ
電車Qの速さは,分速 ア mより速く,分速 イ mより遅い。 ただし,ア は,あてはまる数のうち最も小さい数,イ は,あてはまる数のうち最も大きい数である。
正解:●●●
4.電車Rは,午前8時14分にC駅を出発し,A駅に向かって一定の速さで進み,B駅とC駅の間で電車Pとすれちがい,午前8時24分にA駅とB駅の間で,A駅から4000m離れている地点を通過する。
このとき,電車Rが電車Pとすれちがったのは,午前8時何分何秒か求めなさい。
正解:●●●
【5】
円Oの円周上に5点A, B, C, D, Eをとり,五角形ABCDEをつくる。
図1は,五角形ABCDEにおいて,点Bと点Eを結び,BE//CDとなる場合を表している。
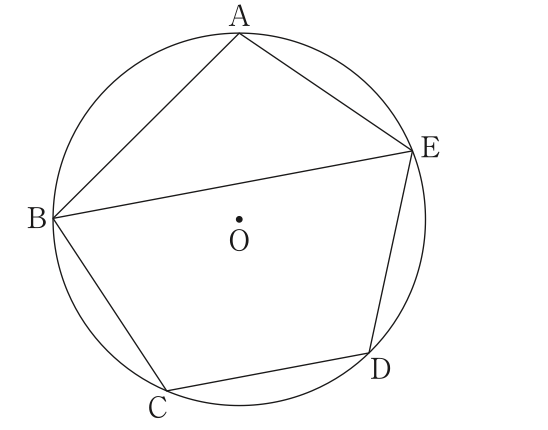
次の1〜3に答えなさい。
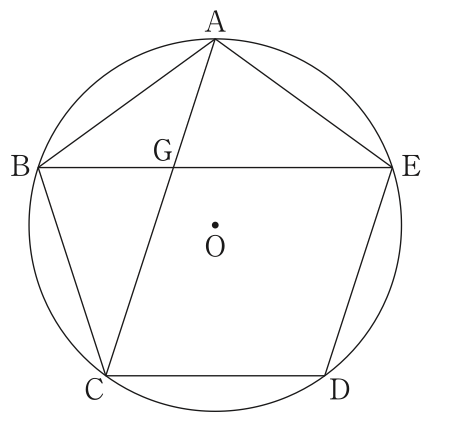
1.図2は,図1において,五角形ABCDEが,正五角形となる場合を表しており,点Aと点Cを結び,線分ACと線分BEとの交点をGとしたものである。
このとき, の大きさを求めなさい。
正解:●●●
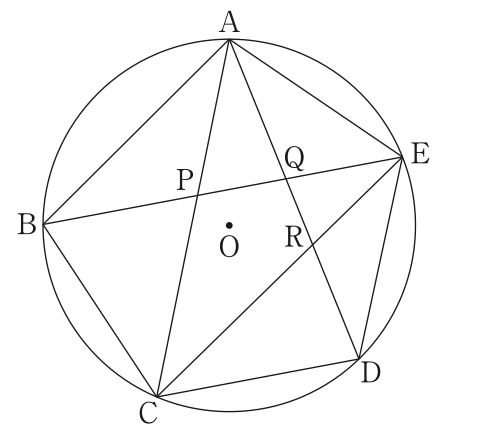
2.図3は,図1において,点Aと点C,点Aと点D,点Cと点Eを結び,線分BEと線分AC,線分ADとの交点をそれぞれP,Qとし,線分ADと線分CEとの交点をRとしたものである。
図3において, であることを証明しなさい。
正解例:●●●
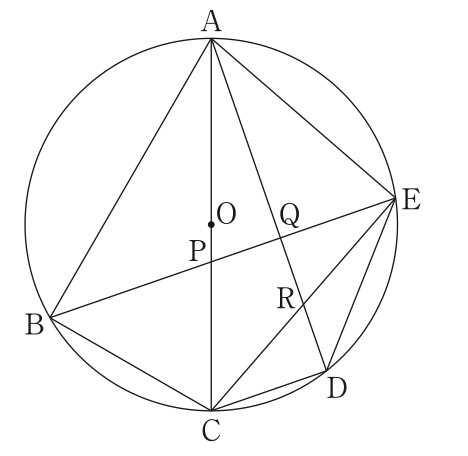
3.図4は,図3において, ,AP:PC=3:2,線分ACが円Oの直径となる場合を表している。
図4において,AE=6cmのとき,円Oの直径を求めなさい。
正解:●●●
【6】
図1は,底面ABCがAB=4cm,BC=3cm, の直角三角形で,側面が全て長方形の三角柱ABCDEFを表しており,AD=6cmである。
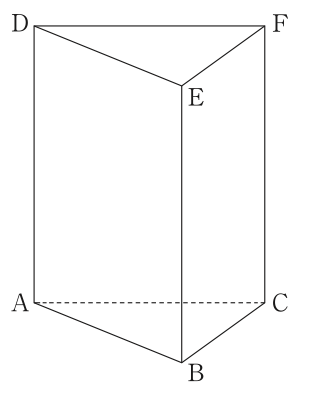
次の1〜3に答えなさい。
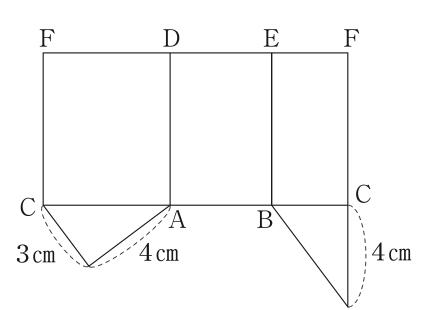
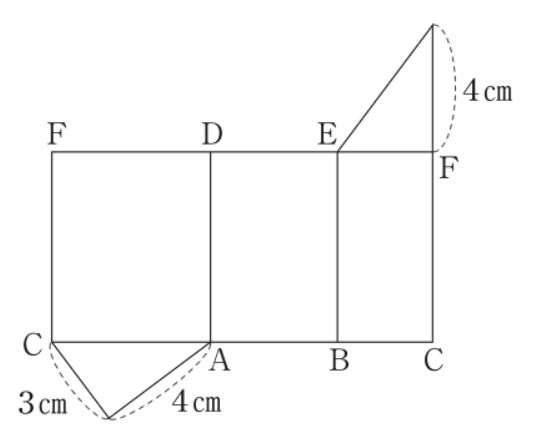
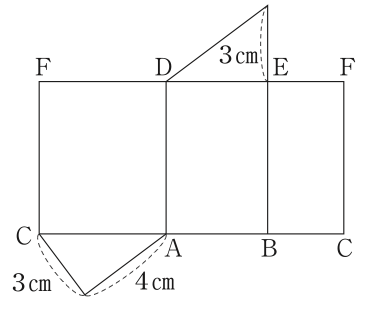
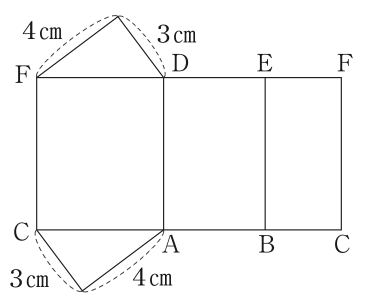
1.図1に示す三角柱の展開図が,次のア〜エに1つある。それを選び,記号をかきなさい。
正解:●●●
2.図1に示す三角柱において,辺AB上に点Pを,AP=1cmとなるようにとり,辺CF上に点Qをとる。PQ=5cmのとき,三角錐QABCの体積を求めなさい。
正解:●●●
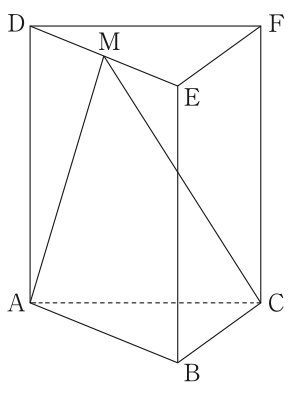
3.図2は,図1に示す三角柱において,辺DEの中点をMとし,点Mと点A,点Mと点Cを結んだものである。線分MC上に点Kを,KC=ACとなるようにとり,線分MA上に点Lを,LK//ACとなるようにとる。
このとき, の面積は, の面積の何倍か求めなさい。
正解:●●●
福岡県教育委員会のホームページより、最新の情報が得られます。必要に応じて、見るようにしましょう!