東京都公立高校入試　2025年　数学

最後に、傾向と対策・高校入試のしくみなどへのLINKがあります。

【１】

次の各問に答えよ。

問1

3 − 6² ÷ 4 を計算せよ。

問2

$\frac{9a-b}{5}-a+2b$ を計算せよ。

問3

(3√7 + 8)(3√7 − 8) を計算せよ。

問4

一次方程式 $\frac{9x-6}{2}=4x+1$ を解け。

問5

連立方程式

• 8x − 5y = −3
• y = 2x − 1

問6

x² − 9x + 7 = 0 を解け。

問7

次の①と②に当てはまる数を、下のア〜クのうちからそれぞれ選び、記号で答えよ。

関数 y = −x² について、x の変域が −2 ≤ x ≤ 3 のときの y の変域は、

• ① ≤ y ≤ ②

選択肢:

• ア: −9
• イ: −6
• ウ: −4
• エ: −2
• オ: 0
• カ: 4
• キ: 6
• ク: 9

問8

次の□の中の「あ」「い」に当てはまる数字をそれぞれ答えよ。

右の図1のように、1, 2, 3, 4, 5の数字を1つずつ書いた5枚のカードがある。

この5枚のカードから同時に3枚のカードを取り出すとき、取り出した3枚のカードに書いてある数の和が10以上になる確率は、

である。ただし、どのカードが取り出されることも同様に確からしいものとする。

問9

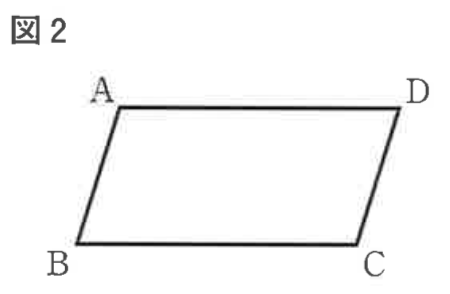
右の図2で、四角形ABCDは平行四辺形である。

解答欄に示した図をもとにして、辺AD上にあり、頂点B、頂点Cまでの距離が等しい点Pを、定規とコンパスを用いて作図によって求め、点Pの位置を示す文字Pも書け。

ただし、作図に用いた線は消さないでおくこと。

正解：
問１ ●●●
問２ ●●●
問３ ●●●
問４ ●●●
問５ ●●●
問６ ●●●
問７ ① ●●●
問７ ② ●●●
問８ ●●●
問９ ●●●

【２】

Sさんのクラスで考えた問題

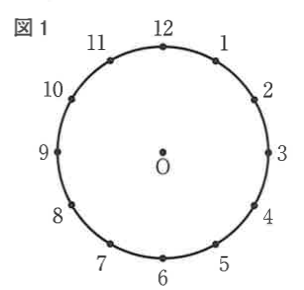
右の図1のように、円Oの円周を12等分する点に、1から12までの自然数の番号を、小さい順で時計回りに付ける。

1から12までの番号を付けた点のうち、2点を結んでできる線分が円Oの直径となるとき、その2点を向かい合う点とする。

例えば、1の点と7の点は、向かい合う点である。

図1において、1組の向かい合う点を選び、それぞれの点の番号のうち、小さい方の数を、大きい方の数をとする。

$a,\; b\; の平均値を\; A\; とし、b^2-a^2の値を\; B\; とするとき、\; B\; は\; A\; の何倍か求めなさい。$

問1

• ア: 3
• イ: 4
• ウ: 6
• エ: 12

Sさんのグループが作った問題

右の図2のように、円Oの円周を24等分する点に、1から24までの自然数の番号を、小さい順で時計回りに付ける。

1から24までの番号を付けた点のうち、2点を結んでできる線分が円Oの直径となるとき、その2点を向かい合う点とする。

図2において、異なる2組の向かい合う点を選び、1組目のそれぞれの点の番号のうち、小さい方の数を、大きい方の数をとし、2組目のそれぞれの点の番号のうち、小さい方の数を、大きい方の数をとする。

$a,b,c,d\mathrm{の平均値を}P\mathrm{とし、}bd-ac\mathrm{の値を}Q\mathrm{とするとき、}Q\; =\; 24P\mathrm{となることを確かめてみよう。}$

問2

［Sさんのグループが作った問題］で、Q＝24Pとなることを証明せよ

解答：

問１　●●●
問２　●●●

【３】

図 1

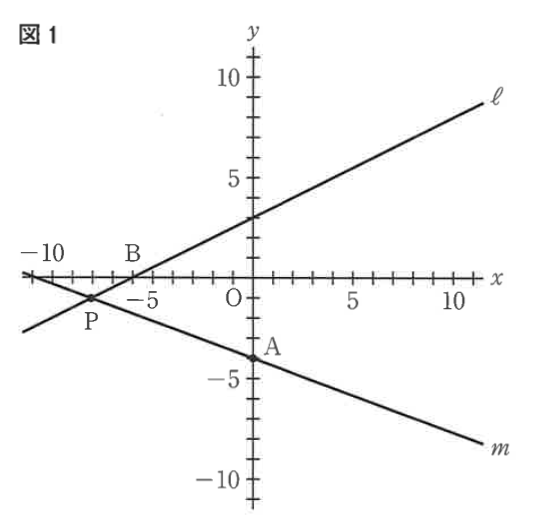
図1で、点Oは原点、点Aの座標は(0, -4)であり、直線ℓは以下の一次関数で表されています。

直線ℓとx軸との交点をBとする。直線ℓ上にある点をPとし、2点A、Pを通る直線をmとする。次の各問に答えよ。

問1

点Pのy座標が-1のとき、点Pのx座標を次のア〜エのうちから選び、記号で答えよ。

• ア: -8
• イ: $–\frac{9}{2}$
• ウ: -2
• エ: $\frac{5}{2}$

問2

点Pが点Bに一致するとき、直線mの式を次のア〜エのうちから選び、記号で答えよ。

• ア: $y=–\frac{3}{2}x–4$
• イ: $y=–\frac{3}{2}x–6$
• ウ: $y=–\frac{2}{3}x–4$
• エ: $y=–\frac{2}{3}x–6$

問３

以下の図と条件に基づいて、点Pのx座標を求めなさい。

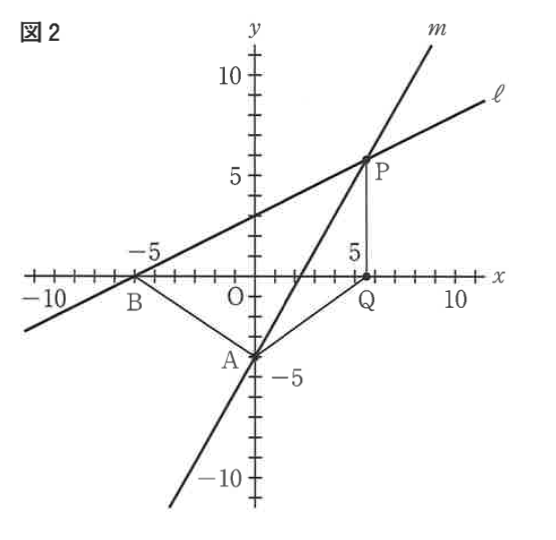
図2は、図1において、点Pのx座標が正の数のとき、x軸上にありx座標が点Pのx座標と等しい点をQとし、 点Aと点B、点Aと点Q、点Pと点Qをそれぞれ結んだ場合を表している。

△APBの面積が△AQPの面積の2倍になるとき、点Pのx座標を求めよ。

解答：
問１　●●●
問２　●●●
問３　●●●

【４】

以下の図を参照してください。

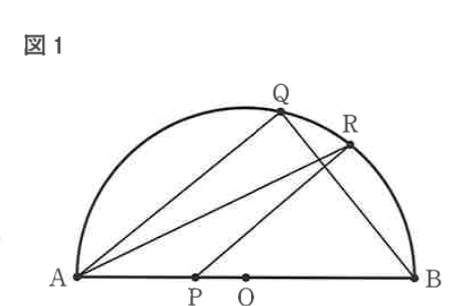
右の図1で、点Oは線分ABを直径とする半円の中心である。

• 点Pは、線分OA上にある点で、点O、点Aのいずれにも一致しない。
• 点Qは、AB上にある点で、点A、点Bのいずれにも一致しない。
• 点Rは、BQ上にある点で、点B、点Qのいずれにも一致しない。

点Aと点Q、点Aと点R、点Bと点Q、点Pと点Rをそれぞれ結ぶ。

問1

図1において、$\mathrm{AQ}=\mathrm{BQ}$、$\angle \mathrm{QAR}=20°$、 $\angle \mathrm{ARP}=a°$とするとき、 $\angle \mathrm{BPR}$の大きさを表す式を、 次のア〜エのうちから選び、記号で答えよ。

1. $a+20°$
2. $a+25°$
3. $155-a$
4. $160-a$

問2

右の図2は、図1において、$AP=AQ,BR=QR$ のとき、点$Q$と点$R$を結んだ場合を表している。

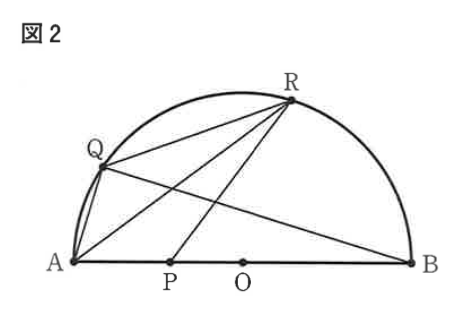
次の①、②に答えよ。

① △APR ≡ △AQRであることを証明せよ。

△APR と △AQR の合同条件を満たすことを証明する。

② 次の【　　】の中の「う」「え」に当てはまる数字をそれぞれ答えよ。

図2において、線分ARと線分BQとの交点をS、点Oと点Rを結び、線分BQと線分ORとの交点をTとした場合を考える。

AP = 20Pのとき、ΔRSTの面積は、四角形AORQの面積の【 $\frac{う}{え}\mathrm{】倍である。}$

正解：
問１　●●●
問２ ①　●●●
②　●●●

【５】

図1に示した立体 $ABCD–EFGH$ は、
$AB=AD=6cm$, の直方体である。
頂点 $A$ と頂点 $C$ を結び、線分 $AC$ 上にある点を $P$ とする。
頂点 $H$ と点 $P$ を結ぶ。
次の各問に答えよ。

問1

次の【　　】の中の「お」「か」に当てはまる数字をそれぞれ答えよ。
図1において、頂点 $D$ と点 $P$、頂点 $E$ と点 $P$ をそれぞれ結んだ場合を考える。
点 $P$ が線分 $AC$ の中点のとき、立体 $P\; –\; AEHDの体積は【おか】㎤である$

問２

次の【　　】の中の「き」「く」「け」に当てはまる数字をそれぞれ答えよ。

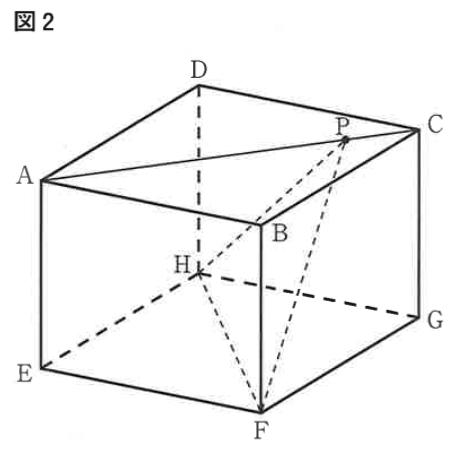
右の図2は、図1において、頂点Fと頂点H、頂点Fと点Pをそれぞれ結んだ場合を表している。

AP : PC = 5 : 1 のとき、
△FPHの面積は、 $\mathrm{きく}\sqrt{け}㎠$ である。

正解：
問１　●●●
問２　●●●

東京都教育委員会のホームページより、最新の情報が得られます。必要に応じて、見るようにしましょう！