最後に、傾向と対策・高校入試のしくみなどへのLINKがあります。

【１】

次の問いに答えなさい。

1. $x=3–\sqrt{2}$ のとき、 $x^2–4x+6$ の値を求めなさい。

2. ${(3x+y)}^2–3x–y–2$ を因数分解しなさい。

3. $a$ 、 $b$ を定数とする。 $x$ 、 $y$ の連立方程式 $\{\begin{array}{c}x+ay=4–2b\\ bx+y=2a\end{array}$ の解が $x=5$ 、 $y=–1$ であるとき、 $a$ 、 $b$ の値をそれぞれ求めなさい。

4. $n$ を自然数とする。 $2\sqrt{n}<\sqrt{x}<3\sqrt{n}$ を満たす自然数 $x$ の個数を $n$ を用いて表しなさい。

5. $a$ 、 $b$ を定数とし、 $a<b$ 、 $c=a+3$ 、 $d=b+3$ とする。関数 $y=\frac{1}{2}{x}^2$ について、次の二つの条件を同時に満たす $a$ 、 $b$ の値をそれぞれ求めなさい。

   • $x$ の変域が $a\le x\le b$ のときの $y$ の変域は $0\le y\le 18$ である。
   • $x$ の変域が $c\le x\le d$ のときの $y$ の変域は $0\le y\le 8$ である。

6. A, B二つのさいころを同時に投げ、Aのさいころの出る目の数を $a$ 、Bのさいころの出る目の数を $b$ とし、 $c=2a+b$ とする。このとき、 $\frac{20}{25}$ の値が自然数である確率を求めなさい。1から6までのどの目が出ることも同様に確からしいものとして答えなさい。

7. $n$ を2けたの自然数とする。次の二つの条件を同時に満たす $n$ の値をすべて求めなさい。

   • $n$ の一の位の数は、 $n^2$ の一の位の数と同じである。
   • $n$ の十の位の数は、70+ $n$ の十の位の数より3大きい。

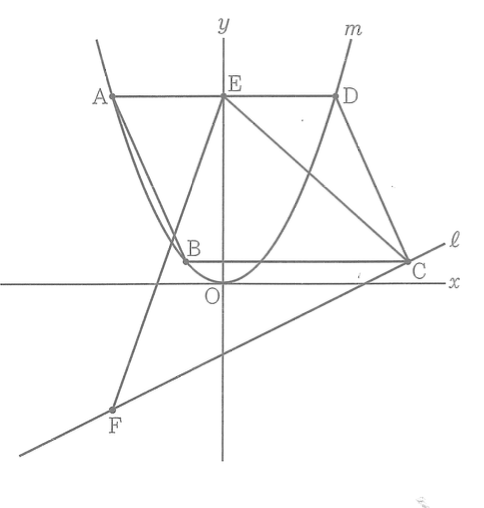
8. 下の図において、 $m$ は関数 $y=a{x}^2$ （ $a$ は定数）のグラフを表す。四角形ABCDは平行四辺形であり、A、B、Dは $m$ 上にある。辺ADは $x$ 軸に平行であって、Aの $x$ 座標は-3であり、Bの $x$ 座標は-1である。Eは、辺ADと $y$ 軸との交点である。EとCを結ぶ。 $l$ は、Cを通り傾きが $\frac{1}{2}$ の直線である。Fは $l$ 上の点であり、Fの $x$ 座標はAの $x$ 座標と等しい。EとFとを結ぶ。四角形ABCDの面積と $▵$ EFCの面積は等しい。 $a$ の値を求めなさい。答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。ただし、原点Oから点(1,0)までの距離、原点Oから点(0,1)までの距離はそれぞれ1cmであるとする。

   

解答
（１）●●●
（２）●●●
（３）aの値●●●　　bの値●●●
（４）●●●
（５）aの値●●●　　bの値●●●
（６）●●●
（７）●●●
（８）●●●

【２】

2

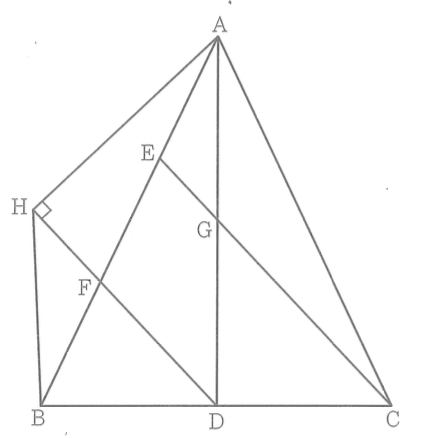
下の図において、 $▵\mathrm{ABC}$ は $\mathrm{AB}=\mathrm{AC}$ の二等辺三角形である。Dは、 $▵\mathrm{ABC}$ の頂角 $\angle \mathrm{BAC}$ の二等分線と辺BCとの交点である。E、Fは辺AB上に会ってA、Bと異なる点であり、 $\mathrm{AE}=\mathrm{EF}=\mathrm{FB}$ である。CとEとを結ぶ。Gは、線分ECと線分ADとの交点である。Hは、Aから直線FDにひいた垂線と直線FDとの交点である。Hは、直線ABについてCと同側にある。HとBとを結ぶ。

次の問いに答えなさい。

1. $▵\mathrm{ABC}$ の内角 $\angle \mathrm{BAC}$ の大きさを $a^{°}$ とするとき、 $▵\mathrm{ABC}$ の頂点Cにおける外角の大きさを $a$ を用いて表しなさい。

2. $▵\mathrm{AHD}\backsim ▵\mathrm{CDG}$ であることを証明しなさい。

3. $\mathrm{AB}=7 \mathrm{cm}$ 、 $\mathrm{BC}=6 \mathrm{cm}$ であるとき、

   1. 線分GCの長さを求めなさい。

   2. $▵\mathrm{AHB}$ の面積を求めなさい。

正解
（１）●●●
（２）●●●
（３）①●●●
　　　②●●●

【３】

3

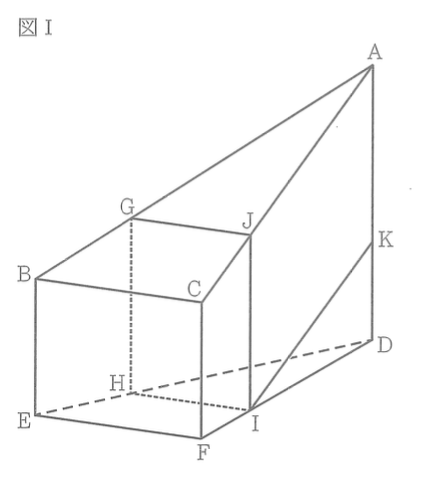
図I、図IIにおいて、立体ABC-DEFは五つの平面で囲まれた立体である。 $▵\mathrm{DEF}$ は $\angle \mathrm{DFE}=90°$ の直角三角形であり、 $\mathrm{DF}=5 \mathrm{cm}$ 、 $\mathrm{EF}=4 \mathrm{cm}$ である。四角形BEFCは長方形であり、 $\mathrm{BE}=3 \mathrm{cm}$ である。四角形CFDAは $\mathrm{CF}\cdot \cdot \cdot \parallel \cdot \cdot \cdot \mathrm{AD}$ の台形であり、 $\angle \mathrm{CFD}=\angle \mathrm{ADF}=90°$ 、 $\mathrm{AD}=6 \mathrm{cm}$ である。四角形BEDAは $\mathrm{BE}\cdot \cdot \cdot \parallel \cdot \cdot \cdot \mathrm{AD}$ の台形であり、 $\angle \mathrm{BED}=\angle \mathrm{ADE}=90°$ である。このとき、 $▵\mathrm{ABC}$ は $\angle \mathrm{ACB}=\angle \mathrm{ACE}=90°$ の直角三角形である。

次の問いに答えなさい。

1. (1) 図Iにおいて、四角形GHIJは長方形であり、G、H、I、Jはそれぞれ辺AB、BE、DF、AC上にある。このとき、 $\mathrm{GH}\cdot \cdot \cdot \parallel \cdot \cdot \cdot \mathrm{BE}$ 、 $\mathrm{GJ}\cdot \cdot \cdot \parallel \cdot \cdot \cdot \mathrm{BC}$ である。Kは、Lを通り辺ACに平行な直線と辺ADとの交点である。

   

   1. 次のア～オのうち、辺ABとねじれの位置にある辺はどれですか。すべて選びなさい。

      • $ア$ 辺 AD
      • $イ$ 辺 DF
      • $ウ$ 辺 DE
      • $エ$ 辺 EF
      • $オ$ 辺 CF

   2. $▵\mathrm{AGJ}$ の面積は $▵\mathrm{AID}$ の面積の何倍であるか求めなさい。

   3. 辺GJの長さが辺GJの長さより $1 \mathrm{cm}$ 長いときの四角形GHIJの周の長さを求めなさい。

2. (2) 図IIにおいて、Lは辺DF上にあって、線分 $\mathrm{AL}$ の長さと線分 $\mathrm{LE}$ の長さの和が最も小さくなる点である。LとCとを結ぶ。Mは、Lを通り辺DFに平行な直線と辺DEとの交点である。MとA、MとBとをそれぞれ結ぶ。

   

   1. 線分MLの長さを求めなさい。

   2. 立体ABMLCの体積を求めなさい。

１（１）●●●
　（２）●●●
　（３）●●●
２（１）●●●
　（２）●●●

大阪府教育委員会のホームページより、最新の情報が得られます。必要に応じて、見るようにしましょう！