最後に、傾向と対策・高校入試のしくみなどへのLINKがあります。
【1】
計算問題
次の計算をしなさい。
-
-
-
-
-
-
正解:
(1)●●●
(2)●●●
(3)●●●
(4)●●●
(5)●●●
(6)●●●
問題内容
次の問いに答えなさい。
(1) のとき、 の値を求めなさい。
(2)次のア〜エのうち、無理数であるものはどれですか。一つ選び、記号を〇で囲みなさい。
(3)比例式
を満たす
の値を求めなさい。
(4)次のア〜エのうち、 が
に反比例するものはどれですか。一つ選び、記号を〇で囲みなさい。
- ア: 1本の値段が100円のペンを 本買ったときの代金円
- イ: 30枚の色紙から枚を使ったときの残りの色紙の枚数
- ウ: 1500mの道のりを分速 mで歩いたときにかかる時間分
- エ:
mLのお茶を5人で同じ量に分けたときの一人当たりのお茶の量 mL
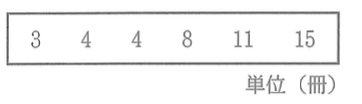
(5) 次のデータは、6人の生徒それぞれが1学期に読んだ本の冊数を値の小さい順に並べたものである。6人の生徒それぞれが読んだ本の冊数の範囲を求めなさい。
(6) 連立方程式を解きなさい。
(7) 二つの箱 A、B がある。箱 A には奇数の書いてある3枚のカード 1、3、5 が入っており、箱 B には偶数の書いてある3枚のカード 4、6、8 が入っている。A、B それぞれの箱から同時にカードを1枚ずつ取り出すとき、取り出した2枚のカードに書いてある数の和が 7 である確率はいくらですか。A、B それぞれの箱において、どのカードが取り出されることも同様に確からしいものとして答えなさい。
(8) 二次方程式を解きなさい。
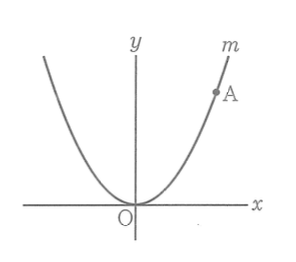
(9) 右の図において、m は関数
(a は定数) のグラフを表す。A は m 上の点であり、その座標は (5, 7) である。a の値を求めなさい。
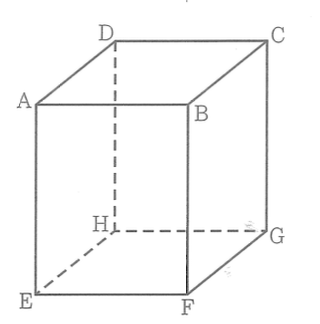
(10) 右の図において、立体 ABCDEFGH は直方体であり、AB = AD = 4cm、AE = 5cm である。
① 次のア~エのうち、辺 AE とねじれの位置にある辺はどれですか。一つ選びなさい。
ア 辺 AB イ 辺 BF ウ 辺 EH エ 辺 FG
② 立体 ABCDEFGH の表面積を求めなさい。
正解:
(1)●●●
(2)●●●
(3)●●●
(4)●●●
(5)●●●
(6)●●●
(7)●●●
(8)●●●
(9)●●●
(10)① ●●●
② ●●●
【3】
体育祭の準備
体育祭の準備のため、Fさんはグラウンドで先生と一緒に、杭を打ってロープを張ることになった。
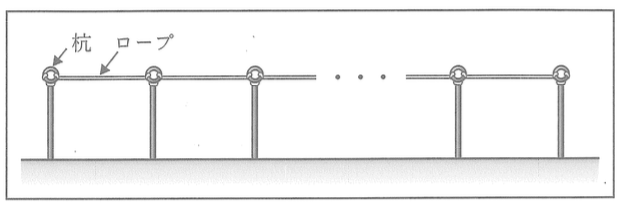
ロープは、それぞれの杭の上部にある輪に結びながら張っていく。杭に結ぶ部分のロープの長さはすべて 20cm であり、ロープはたるみなく張るものとする。
Fさんは、杭を 100cm 間隔で打ってロープを張ることにした。下の図は、Fさんが使ったロープを表す模式図である。「杭の本数」が
x 本のときの「使ったロープの長さ」を
y cm とする。
x=2 のとき
y=140 であるとし、
x の値が 1 増えるごとに
y の値は 120 ずつ増えるものとする。
次の問いに答えなさい。
(1) 次の表は、
x と
y との関係を示した表の一部である。表中の (ア) 、 (イ) に当てはまる数をそれぞれ書きなさい。
| x |
2 |
3 |
4 |
… |
7 |
… |
| y |
140 |
260 |
(ア) |
… |
(イ) |
… |
(2)
x を 2 以上の自然数として、
y を
x の式で表しなさい。
(3)
y=1580 となるときの
x の値を求めなさい。
正解:
(1)ア●●●
イ●●●
(2)●●●
(3)●●●
【4】
図形問題
次の図において、△ABCは∠ABC=90°の直角三角形であり、AB=3cmである。Dは、辺AC上にA、Cと異なる点である。△EDB≡△ADBであり、DE∥BCである。Fは、辺EBと辺ACとの交点である。BC=xcmとし、x>0とする。
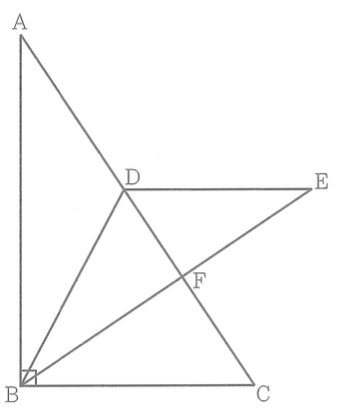
(1)
△ADBを、ある直線を対称の軸として対称移動すると、△EDBにぴったり重ねることができる。次のア~エの直線のうち、このときの対称の軸はどれですか。一つ選びなさい。
- ア 直線 DB
- イ 直線 AB
- ウ 直線 AC
- エ 直線 DE
(3)
次は、△ABC∽△BFCであることの証明である。( a )( b )に入れるのに適している「角を表す文字」をそれぞれ書きなさい。また、c〔 〕から適しているものを一つ選びなさい。
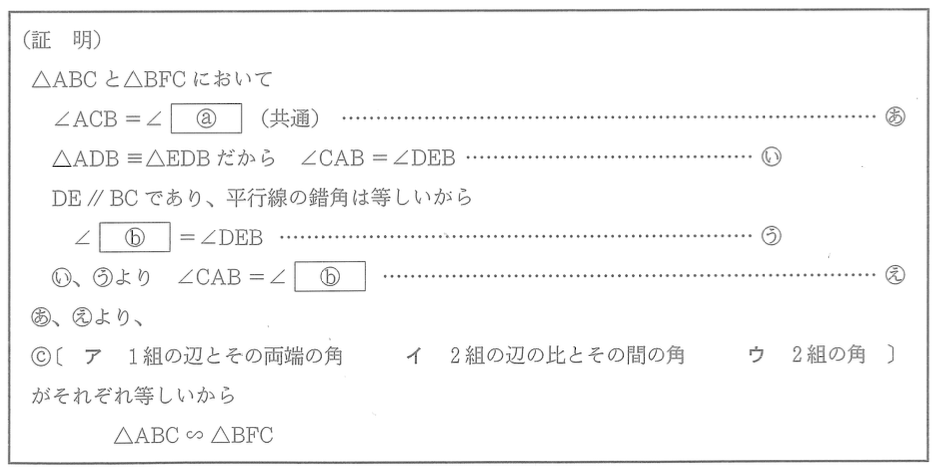
(4)
x=2であるときの線分BFの長さを求めなさい。答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。
正解:
(1)●●●
(2)●●●
(3)a●●●
b●●●
c●●●
(4)●●●
大阪府教育委員会のホームページより、最新の情報が得られます。必要に応じて、見るようにしましょう!