最後に、傾向と対策・高校入試のしくみなどへのLINKがあります。

【１】

次の計算をしなさい。

解答：
(1)●●●
(2)●●●
(3)●●●
(4)●●●
(5)●●●

【２】

解答：
(1)●●●
(2)●●●
(3)●●●
(4)●●●

解答：
(5)●●●
(6)●●●
(7)●●●
(8)●●●

【３】

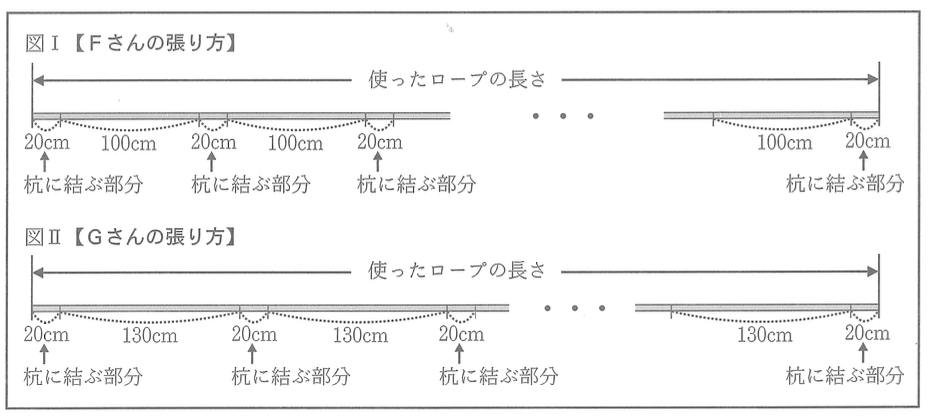
Fさんは、杭を100 cm間隔で打ってロープを張ることにした。図Iは、Fさんが使ったロープを表す模式図である。「杭の本数」が2本のとき「使ったロープの長さ」は140 cmであるとし、「杭の本数」が1本増えることに「使ったロープの長さ」は120 cmずつ長くなるものとする。（これを【Fさんの張り方】とする。）

Gさんは、杭を130 cm間隔で打ってロープを張ることにした。図IIは、Gさんが使ったロープを表す模式図である。「杭の本数」が2本のとき「使ったロープの長さ」は170 cmであるとし、「杭の本数」が1本増えることに「使ったロープの長さ」は150 cmずつ長くなるものとする。（これを【Gさんの張り方】とする。）

次の問いに答えなさい。

(1) 【Fさんの張り方】において、「杭の本数」が$x$本のときの「使ったロープの長さ」を$y$ cmとする。

① 次の表は、$x$と$y$との関係を示した表の一部である。表中の(ア)、(イ)に当てはまる数をそれぞれ書きなさい。

② $x$を2以上の自然数として、$y$を$x$の式で表しなさい。

③ $y=1580$となるときの$x$の値を求めなさい。

(2) Fさんは【Fさんの張り方】で$s$本の杭を打ってロープを張り、Gさんは【Gさんの張り方】で$t$本の杭を打ってロープを張った。2人が打った杭の本数の合計が38本であり、Fさんが使ったロープの長さとGさんが使ったロープの長さが同じであるとき、$s$、$t$の値をそれぞれ求めなさい。

解答：
(1)①ア●●●
　　 イ●●●
　②●●●
　③●●●
(2)●●●

数学問題

[I]

図Iにおいて、A, B, Cは点Oを中心とする円の周上の異なる3点である。3点A, B, Cを結んでできる△ABCはAB = ACの二等辺三角形であり、頂角∠BACは鋭角である。Dは、Bから線分ACにひいた垂線と線分ACとの交点である。Eは、直線OCと円Oとの交点のうちCと異なる点である。Fは、線分ECと線分ABとの交点である。EとAを結ぶ。

次の問いに答えなさい。

1. △EAC ≡ △CDBであることを証明しなさい。
2. AB = 5cm, DC = 2cmであるとき、
   1. 線分BDの長さを求めなさい。
   2. 線分AFの長さを求めなさい。

[Ⅱ]

図Ⅱにおいて、立体A–BCDEは四角すいであり、直線ABは平面BCDEと垂直である。AB = 3cmである。四角形BCDEは長方形であり、BC = 5cm, BE = 4cmである。Fは、辺AE上の点である。Gは、Fを通り辺DEに平行な直線と辺ADとの交点である。GとEを結ぶ。Hは、Gを通り辺CDに平行な直線と辺ACとの交点である。HとBを結ぶ。このとき、4点H, G, E, Bは同じ平面上にある。

次の問いに答えなさい。

3. 次のア〜エの角のうち、その大きさが90°であるものはどれですか。すべて選びなさい。
   • ア: △ACDの内角∠ACD
   • イ: △ACDの内角∠ADC
   • ウ: △ADEの内角∠ADE
   • エ: △ADEの内角∠AED
4. FE = 3cmであるとき、
   1. △HCBの面積を求めなさい。
   2. 立体AHGEBの体積を求めなさい。

解答：
（Ⅰ）
(1)●●●
(2)①●●●
②●●●
（Ⅱ）
(3)●●●
(4)①●●●
②●●●

大阪府教育委員会のホームページより、最新の情報が得られます。必要に応じて、見るようにしましょう！