
【1】
次の問に答えなさい。
(1) 次の⬜︎にあてはまる数を求めなさい。
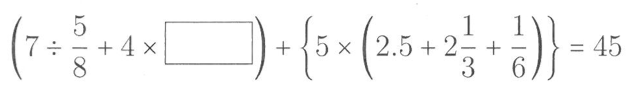
(2) 容器Aには20%の食塩水が50g、容器Bには15%の食塩水が40g入っています。AからBに食塩水を何gか移して、それぞれの食塩水にとけている食塩の重さが同じになるようにしました。このとき、Bに入っている食塩水の濃度を求めなさい。
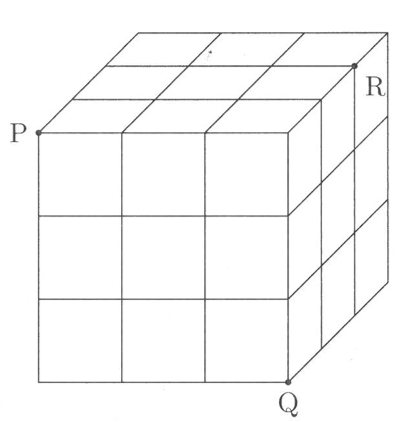
(3) 次の図のように、1辺の長さが1cmの立方体を27個組み合わせてできた1辺の長さが3cmの立方体があります。この立方体を3点P, Q, Rを通る平面で切断するとき、1辺の長さが1cmの立方体は何個切断されるか求めなさい。
正解:
(1)●●●
(2)●●●
(3)●●●
(4) A, Bの2人が地点Pから地点Qを通り、Qから1800m離れた地点Rまで進みます。Aは分速60m、Bは分速48mでPを同時に出発し、それぞれQに着いたら速さを変えてRまで進みます。AはBより5分早くQに着き、BはPを出発して35分後にRに着きました。このとき、BはQからRまで分速何mで進んだか求めなさい。
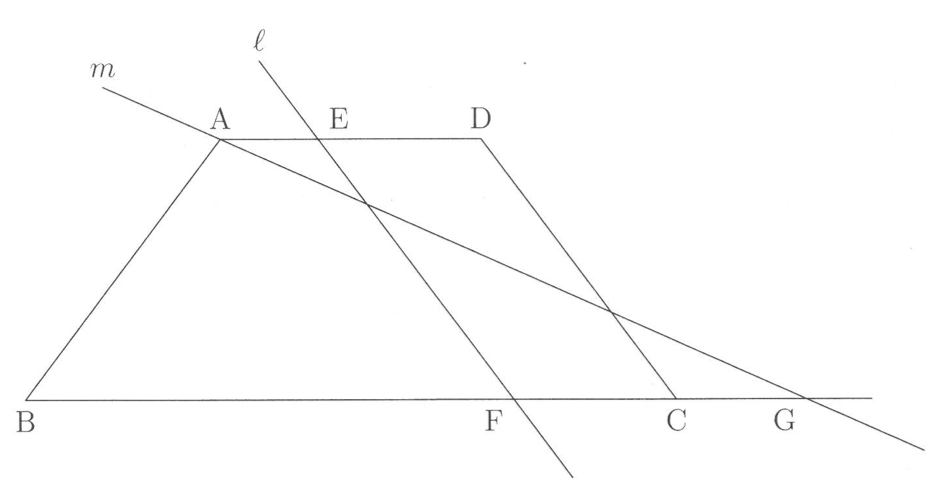
(5) 次の図のように、ADとBCが平行でAB = DCである台形ABCDがあります。DCに平行で台形ABCDの面積を二等分する直線lを引き、lとAD, BCの交点をそれぞれE, Fとします。また、Aを通り、平行四辺形EFCDの面積を二等分する直線mを引き、mと直線BCの交点をGとします。FCの長さが4cm、CGの長さが2cmのとき、BFの長さを求めなさい。
正解:
(4)●●●
(5)●●●
【2】
ある日、遊園地の入場券を買うために 200人が並んでいました。この遊園地には1分あたり7人に入場券を販売する窓口があり、9時から販売を始めました。また、入場券を販売し始めてから最初の30分間は1分あたり3人ずつ、次の20分間は1分あたり10人ずつ並びました。さらに、次の30分間は1分あたり3人ずつというように、この30分間と20分間の並び方が浸量に繰り返されました。このとき、次の問いに答えなさい。
(1) 10時に並んでいた人数を求めなさい。
(2) 並んでいた人が初めていなくなったのは何時何分か求めなさい。
(3)販売を始めた後、途中から新たに1分あたり5人に入場券を販売する窓口を追加したところ、並んでいた人が10時に初めていなくなりました.窓口を追加したのは何時何分か求めなさい。
正解:
(1)●●●
(2)●●●
(3)●●●
【3】
月曜日から金曜日までの5日間の時間割を作ります。
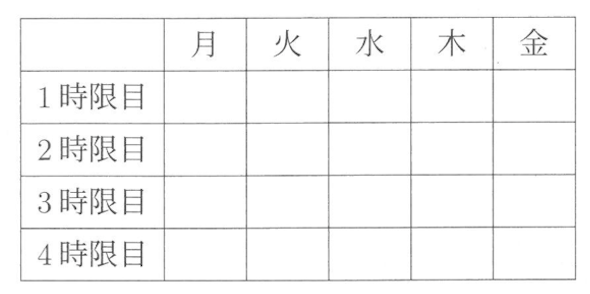
この時間割には国語、算数、理科、社会の4教科が次の<ルール>にしたがって入ります。ただし、1日の時間割は4時間日までとします。
<ルール>
算数は毎日2時間ある。
国語、理科、社会は、それぞれ5日間で3時間以上ある。
水曜日には国語と社会がある。
理科はすべて4時間目のみにある。
国語,社会は、それぞれ1日2時間以上あったとき、その教科は次の日にはない。
1日の中で同じ教科が連続することはない。
このとき、次の問いに答えなさい。
(1) 水曜日の時間割が1時間目算数,2時間目 社会,3時間目 国語,4時間目算数であるとき、火曜日の時間割として適当なものを次のア〜エから1つ選びなさい。
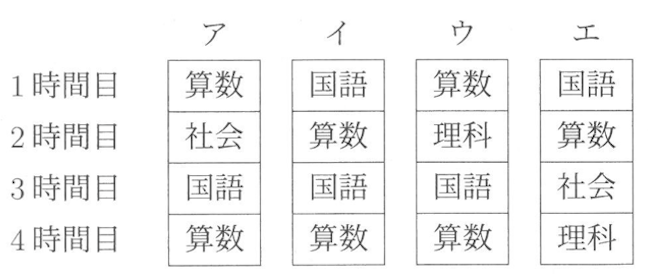
正解:
(1)●●●
(2) 月曜日の時間割が1時間日 算数、2時間目 国語、3時間目算数、4時間目国語であるとします。
(i) 火曜日の時間割を答えなさい。
(ii) 時間割は何通り作ることができるか求めなさい。
正解:(2)
(ⅰ)●●●
(ⅱ)●●●
【4】
次の図のような点Aを中心とする半径3cmの円と点Bを中心とする半径5cmの円があります。これらの円の内側や外側にくっつきながら、中心をP,Q,Rとする半径1cmの3つの円が次の<ルール>にしたがって動きます。以下、この5つの円をそれぞれ円A,B,P,Q,Rと表します。
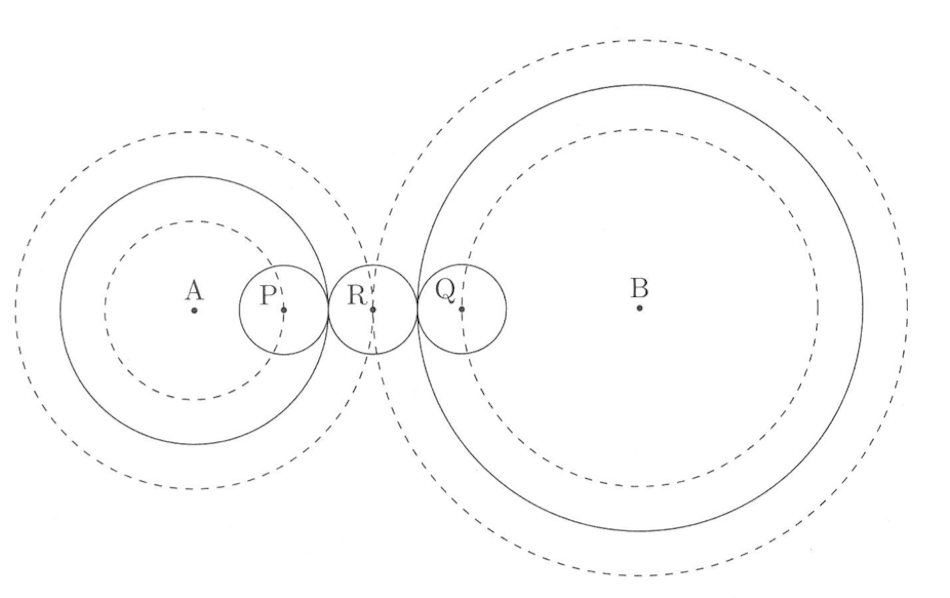
<ルール>
① 上の図のように、最初の位置では、5点A,B,P,Q; Rは一直線上にある。
② 中心Pは点Aを中心とする半径2cmの円周上を反時計まわりに動き続ける。
③ 中心Qは点Bを中心とする半径4cmの円周上を反時計まわりに動き続ける。
④ 中心Rは点Aを中心とする半径4cmの円周上を反時計まわりに一周し、次に点Bを中心とする半径6cmの円周上を時計まわりに一周する.これを繰り返す。
⑤ 3点P,Q,Rは秒速3.14cmで動く。
このとき、次の問いに答えなさい。
(1) 円P,Q, Rが最初の位置と初めて同じ位置にくるのは動き始めてから何秒後か求めなさい。
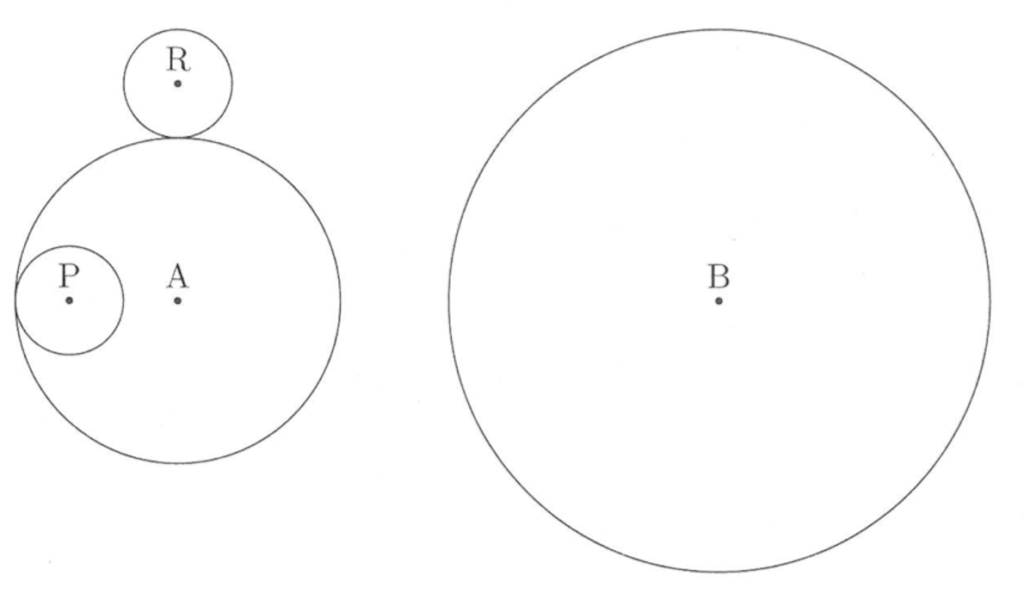
(2) 次の図は、動き始めてから42秒後の円A,B,P,Rの位置を表しています. このときの中心のを作図し、点の近くに「Q」と書きこみなさい。ただし、コンパスを使用して円や円の一部をかくことは1回以下とします。
(3) 2024秒から 2025秒の間に、角RQBの大きさが160°となりました。このとき、角PABの大きさを求めなさい。
正解:
(1)●●●
(2)●●●
(3)●●●
【5】
次の図のようなマスに駒を置いて、次のくルール>にしたがって駒を動かしていきます。

<ルール>
① 駒が置かれたマスに書かれている数字の約数の個数が奇数個のときは1つ右のマスへ駒を動かす。
② 駒が置かれたマスに書かれている数字の約数の個数が偶数個のときは2つ右のマスへ駒を動かす。
例えば、初めに駒が12のマスに置かれたとき、駒は
12のマス→ 14のマス → 16のマス →17のマス→……..
と動きます.初めに1のマスに駒を置いて動かしたとき、次の問いに答えなさい.
(1) 1から20のマスのうち、駒が置かれたマスは何マスか求めなさい。
(2) 駒が100回目に置かれたマスに書かれている数字を求めなさい.ただし、初めに1のマスに駒を置いたときを1回目とします。
(3) 101から 200のマスのうち、駒が置かれなかったマスに書かれている数字をすべてかけたとき、一の位から0が何個連続して並ぶか求めなさい。
正解:
(1)●●●
(2)●●●
(3)●●●



